Valor absoluto
Resumen
En este trabajo encontrarás el significado de valor absoluto, su representación y realización de operaciones con fracciones y enteros, positivos y negativos con igualdad y desigualdad.
Palabras clave: Absoluto, Real, Símbolo, Sustitución, Valor
Abstract
In this work will find the meaning of absolute value, their representation and operations with fractions and integers, positive and negative equality and inequality.
Keywords: Absolute, Real, Symbol, Substitution, Value
Valor absoluto
El valor absoluto lo conocemos como los no negativos y significa quitar el signo negativo y como resultado es que todos los números son positivos, se representan con dos líneas verticales y paralelas, dentro de estas dos líneas paralelas se colocan los números: |x| , se pueden hacer operaciones y estableciendo una igualdad o desigualdad: |x|= a, |x|≥a, |x|≤a, |x|>a, |x|<a
El valor de un número real (a): se define como el número mismo (a)
Si a es positivo, (a) será positivo
Si a es negativo, (a) será positivo
Se representa el valor absoluto con dos líneas paralelas y verticales (| |) ejemplo:
| a | =a.
Si | -5 | = 5
| 5 | = 5
El valor absoluto de:

Entonces podemos establecer que:
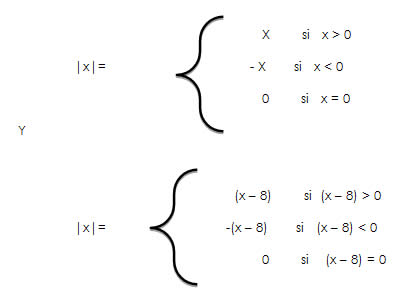
Para todos los valores reales de a, | a | representan un número no negativo
El símbolo de √a :
a = símbolo de un número positivo
y lo definimos como el número positivo cuyo cuadrado es a
Así que √9, a = 3, no – 3
Ahora:
Si √a2 = a, además siendo a positivo; pero √a2 = -a, si a es negativo.
EJEMPLO:
Si a = - 5
√a2 = √(- 5)2 = (- 5) = -a
Otra manera:

Entonces todos los casos se pueden escribir:
√(x - 8)2= |x – 8|
EJEMPLO:
Hallar el conjunto de solución para P, si P = { | | x + 4| = 10}
Esta expresión se lee: Hallar todos los números reales de x, tal que ( | ) el valor
absoluto de (x + 4) sea igual a 10.
Al analizarlo de una manera lógica e inteligente, nos encontramos que la solución
es: x = 6, o bien, x = – 14 y lo demostramos:
|x + 4| = 10
Para x = 6, tenemos que se sustituye el valor de 6 en x:
| 6 + 4 |= 10
| 10 | = 10
10 = 10
Ahora para x = – 14
| – 14 + 4 | = -10
| -10 | = 10
10= 10
| x + 4 | = 10, tiene el mismo conjunto de soluciones que:
(x + 4) = 10, si (x + 4) ≥ 0
O como: – (x + 4) = 10, si (x + 4) < 0 esto equivale a:
x = 6 si x ≥ – 4
x = –7 si x < – 4
Simplificando:
x = 6, o bien, x = – 14; así P = {6, –14}
EJEMPLO:
Encontrar miembros del conjunto z, si z = {x | |x – 3 | > 4}
Después de probar varios substitutos de x, parece ser de cualquier número mayor
que 7 o menor que –1 hace que la aseveración sea cierta:
{ x | |x – 3, > 4 } = { x | x – 3 > 4 si x – 3 ≥ 0 ó – (x – 3) > 4 si x – 3 < 0 }
= {x | | >7 si x ≥ 3 ó x < – 1 si x = 3}
= {x | x > 7 ó x < – 1}
ACTIVIDAD
Instrucciones: Resuelve los siguientes ejercicios propuestos:
1. Escribe la expresión que incluya el valor absoluto y sea equivalente a:
– 3 < x < 5
2. Hallar los dos números reales que encuentra a x, si:
5 < (2x – 3) < – 10
3. Entre qué número estará x, si | x | > 5
4. Entre qué números estará x | | x-4 | = 5
5. Encontrar el conjunto de soluciones para cada una de las expresiones:
- {x | | x – 2 | = 5}
- { y | | y | + y >= 4 }
- {n | | n/(n-2) < 2}
- {x | | 3 – x | > 4}
- {x | | 1/x | = 4}
Referencias bibliográficas
Flores, M. A. (2010). Geometría Analítica. mexico: ESFINGE.
Linares, I. S. (2012). Geomtría Analítica. Mexico: BookMart.
Middlemiss, R. R. (1994). Geometría Analítica. Mexico: Mc.Graw.Hill.
[a] Profesor Investigador de la Universidad Autónoma del Estado de Hidalgo