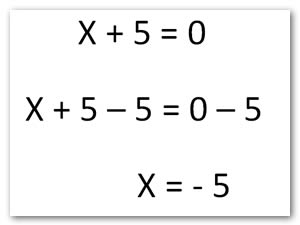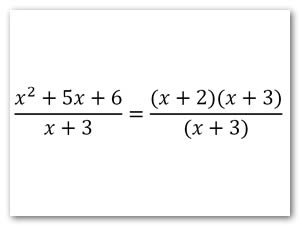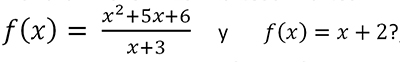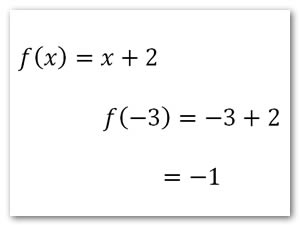La función racional y su dominio
Resumen
En este trabajo se pretende analizar una función racional a partir de la obtención del dominio considerando los algoritmos más comunes en Cálculo Diferencial asignatura que se cursa en cuarto semestre del bachillerato de nuestra máxima casa de estudios de la Universidad Autónoma del Estado de Hidalgo.
Palabras clave: función, dominio, factorización, algoritmo y simplificación.
Abstract
This work intends to analyze a rational function from obtaining the domain, whereas the most common algorithms in calculus differential subject that is studied in the fourth semester of the Bachelor of our maximum house of studies of the Universidad Autónoma del Estado de Hidalgo.
Keywords: function, domain, factoring, algorithm and simplification.
INTRODUCCIÓN
Una de la problemática que radica en las funciones racionales es la obtención de su dominio. De la asignatura de cuarto semestre de Cálculo Diferencial son sin duda las que se simplifican y ya no se presenta la indeterminación. Por otra parte, nuestros estudiantes si llegan a determinar correctamente el dominio de la función por citar caso particular en la cual no se simplifica:
Ya que para su determinación del dominio utilizan el procedimiento:
Paso 1: se analiza si se puede simplificar la función es decir si se puede transformar sin cambiar su valor utilizando los casos de factorización o la división.
Paso 2: igualan a cero el denominador para determinar qué número o números hacen ser cero al denominador.
Paso 3: al determinar dichos números establecen su dominio.
Para la función antes citada los pasos a seguir:
Como no se puede simplificar o transformar se procede a igualar a cero para determinar los valores donde la función no tiene sentido.
Posteriormente el alumno establece que su dominio para esta función es X pertenece a todos los números reales excepto el – 5 de manera abreviada seria X ∈ R excepto-5.
Por lo general la mayoría de los ejercicios y por citar uno de los libros de Cálculo con Geometría Analítica que a mi juicio emplea este algoritmo es: Dennis G. Zill pag. 37. Por otra parte este mismo autor define en la pag. 29 al Dominio de una función f es el conjunto más grande de números reales para el cual es la regla tiene sentido.
Si se le plantea la siguiente función al alumno para que determine el dominio:
Si realizamos el procedimiento seria:
Primero analizamos si se pude simplificar que en este caso particular si se presente y quedaría:
Entonces nuestra función se transforma a f(x)=x+2 y nuestro alumno analiza que su dominio de esta función son todos los números reales ya que es una función de primer grado y que da como imagen una recta y si evalúa obtiene valores con sentido y empleando su calculadora.
Las preguntas serían ¿Qué pasaría si el alumno evalúa con – 3 en ambas funciones:
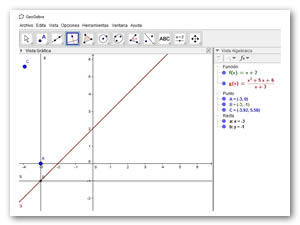
Si utilizamos el GeoGebra para la obtención de la gráfica de ambas funciones por que da la misma imagen.
Si evaluamos en nuestra primera función de partida cuando X= - 3 y empleando nuestra calculadora obtendríamos:
Pero en la otra función obtenemos:
Con estos resultados obtenidos qué opinas del dominio de esta función. Y porque con otros valores distintos de – 3 da el mismo resulta (Zill, 1987)do en ambas.
CONCLUSIÓN
Este tipo de función es la que más requiere sin duda más conocimiento ya que utilizamos el álgebra (resolución de ecuaciones de primer grado y de segundo, despeje de variables, factorización y en ciertos casos la fórmula general). Por otra parte, recuerda que en este tipo de funciones tienes que buscar donde se hace cero en tu denominador.
Referencias
Zill, D. (1987). Cálculo con Geometría Analítica. México: Iberoamericana.
[a] Profesor de Investigación de la Escuela Preparatoria Número 4
Compartir en: