Propuesta para la generación de laberintos ampliados en 2d
Resumen
En el presente trabajo se hace el análisis de los algoritmos más comunes para la construcción de Laberintos de Conexión Simple (LCS): Prim´s, Kruscal, Aldous Broder, Recursivo Backtracker, y Anderson, estos algoritmos generan laberintos de una sola pista, y su desventaja es que permiten tener un número reducido de movimientos. Se utilizan los algoritmos de construcción previos para generar laberintos ampliados, estos laberintos permiten tener una mayor movilidad y direccionalidad al recorrerlos. Se propone el algoritmo llamado “LCSyM Ampliados” cuya principal característica es el cálculo del número de filas y columnas del nuevo laberinto, que basándose en la construcción de LCS se va construyendo uno similar con pasillos ampliados, el cual funciona para cualquier algoritmo de construcción de laberintos analizados.
Palabras clave: algoritmos de construcción LCS, laberintos ampliados
Abstract
Presently work is made the analysis of the most common algorithms for the construction of Simply-Connected Mazes (SCM): Prim's, Kruscal, Aldous Broder, Recursive Backtracker, and Anderson, these algorithms generate labyrinths of a single track, and their disadvantage is that they allow to have a reduced number of movements. The previous construction algorithms are used for this way to generate enlarged maze, these labyrinths allow to have a bigger mobility and directionality when traveling them. Proposed algorithm called "extended SCMyM" whose main characteristic is the calculation of the number of rows and columns of the new labyrinth that being based on the construction of the labyrinths SCM leaves building one similar with wide aisles and proprieties enlarged mazes, which works for any algorithm of construction of analyzed mazes.
Keywords: expanded mazes, mazes construction algorithms SCM
Introducción
Los laberintos rectangulares son de los más utilizados en diferentes campos como lo es la robótica, educación, medicina y entretenimiento [1]-[5], [8], [9]. Existen varios algoritmos para generarlos [1] [2], [12], en este documento se realiza una descripción de los algoritmos más utilizados para la construcción de laberintos de conexión simple (LCS). También se describe una propuesta para generar LCS con pasillos ampliados en 2D, estos laberintos brindan una mayor movilidad y direccionalidad al recorrerlos, permitiendo tener laberintos de diferente complejidad. Se muestran los resultados obtenidos de la propuesta realizada.
Tipos de laberintos
Laberinto de conexión simple (LCS)
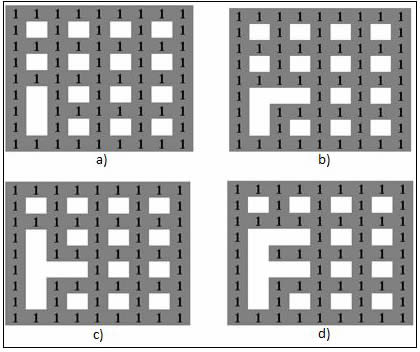
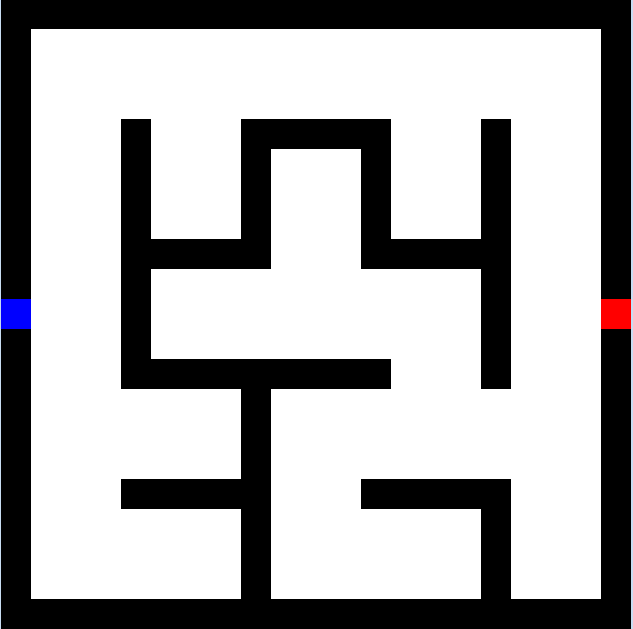
Son aquellos que tienen puntos muertos o callejones sin salida, por lo tanto, solo tienen una solución entre la entrada y la salida, en el proceso de buscar tal solución, en ocasiones, se recorre gran parte del laberinto, causando frustración en el espectador, (ver fig. 1a).
Laberinto de conexión múltiple (LCM)
Son aquellos que tienen más de una solución desde la entrada a la salida. En este tipo de laberintos, además de encontrar una solución, se requiere que sea la más corta. Tienen ciclos internos, lo que dificulta aún más el proceso de buscar la solución, ya que se debe tomar en cuenta en que secciones del laberinto ya se ha transitado, evitando dar giros en un mismo segmento del laberinto, (ver fig. 1b). Sin embargo, en ocasiones, llegan a tener callejones sin salida, en ese caso, se les llaman LCM mixtos, (ver fig. 1c).
a) Laberinto conexión simple
b) Laberinto conexión múltiple
c) Laberinto de conexión múltiple mixto
La construcción de un laberinto puede ser tan complicada como el resolverlo, los laberintos a realizar son de tipo cuadriculado o rejilla, éste debe ser perfecto y completamente conectado, es decir, se debe poder elegir cualquier punto del laberinto como entrada y cualquier otro punto como salida [1],[2],[6],[7].
Construcción de laberintos de conexión simple
La construcción al azar permite generar gran cantidad de laberintos conteniendo corredores como las ramas de un árbol, persiguiendo la desorientación del explorador, siendo a su vez ésta la forma más fácil de implementarse en un programa de computadora. Los algoritmos explicados a continuación, generan laberintos LCS completamente conectados [1] [2].
La construcción al azar se basa en dos enfoques, los cuales se enuncian a continuación:
Cavar túneles. Como su nombre lo indica, se refiere a cavar túneles a lo largo y ancho del laberinto hasta cubrirlo en su totalidad, como la explotación de una mina. A este tipo de construcción, pertenecen:
- Algoritmo de construcción Kruscal.
- Algoritmo de construcción Aldous-Broder.
- Algoritmo de construcción Prim’s.
- Algoritmo de construcción Recursivo Bactracker.
- Algoritmo de construcción de Anderson.
Levantar muros. Consiste en elevar los muros de los corredores por todo el cuerpo del laberinto, como en la construcción de un edificio.
Algoritmo de construcción kruskal
- Especificar el tamaño o las dimensiones del laberinto de acuerdo con las habitaciones que se desea que contenga.
- Dividir el laberinto en habitaciones en base a sus dimensiones y etiquetarlas con una identificación única.
- Seleccionar una habitación al azar y cavar un túnel hacia una habitación adyacente (en caso de existir más de una, elegir al azar) sólo si tiene diferente etiqueta, y etiquetar la habitación o habitaciones que se unieron con la identificación de la habitación inicial; repitiendo este proceso hasta que todas las habitaciones tengan la misma etiqueta.
- Marcar la ubicación de la entrada o del punto inicial de la exploración y la ubicación de la salida.
Algoritmo de construcción Aldous-Broder
Es una técnica simple, pero puede llevar gran tiempo la construcción de un laberinto, esto es porque se va moviendo al azar dentro del laberinto sin discriminar las habitaciones con las que ya se cavaron túneles. Los pasos se enuncian a continuación:
- Especificar el tamaño o las dimensiones del laberinto de acuerdo con las habitaciones que se desea que contenga.
- Dividir el laberinto en habitaciones en base a sus dimensiones.
- Elegir al azar una habitación dentro del laberinto.
- Moverse a una habitación vecina adyacente al azar y cavar un túnel hacia la habitación anterior en el caso de que la nueva habitación no sea parte de otro túnel, continuando con este paso hasta que todas las habitaciones sean parte del laberinto.
- Marcar la ubicación de la entrada o del punto inicial de la exploración y la ubicación de la salida.
Algoritmo de construcción recursivo Backtracker
- Especificar el tamaño o las dimensiones del laberinto de acuerdo con las habitaciones que se desea que contenga.
- Dividir el laberinto en habitaciones en base a sus dimensiones y etiquetarlas con una identificación única
- Elegir al azar una habitación dentro del laberinto y empiece a cavar. Siempre cave hacia habitaciones adyacentes que no han sido cavadas, si las hay, si no, regrese a buscar uno, por el túnel ya cavado, hasta encontrar una.
- Repita este procedimiento, mientras no se regrese al punto inicial.
- Marcar la ubicación de la entrada o del punto inicial de la exploración y la ubicación de la salida.
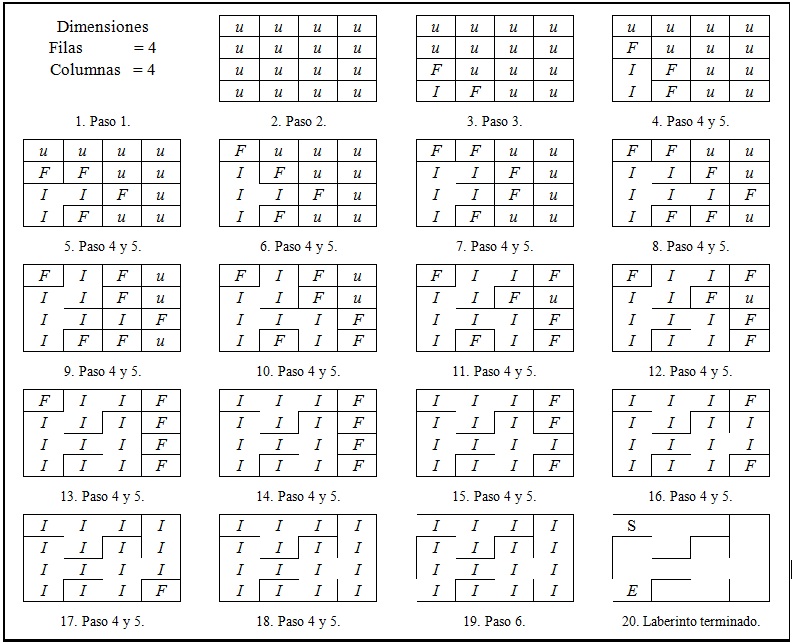
Fig. 2. Construcción de un laberinto con el algoritmo de Prim’s.
Algoritmo de construcción Prim’s
Considera dos tipos de habitaciones:
Habitaciones etiquetadas con I son aquellas que forman parte del laberinto y han sido cavadas.
Habitaciones etiquetadas con F que no han sido cavadas, pero que son adyacentes a una habitación I.
- Especificar el tamaño o las dimensiones del laberinto de acuerdo con las habitaciones que se desea que contenga.
- Dividir el laberinto en habitaciones en base a sus dimensiones y etiquetarlas con una identificación única.
- Seleccionar una habitación inicial, etiquetarla como I y etiquete sus habitaciones adyacentes con F.
- Seleccione una habitación F aleatoriamente. Cavar un muro de la habitación I a la habitación F; cámbielo a I y cambie sus habitaciones adyacentes que no son I a F.
- Repita este proceso mientras haya habitación F.
- Marcar la ubicación de la entrada o del punto inicial de la exploración y la ubicación de la salida.
Por motivos de espacio sólo se hace la representación visual de este algoritmo, (ver fig. 2).
Algoritmo de construcción de Anderson
- Especificar el tamaño o las dimensiones del laberinto de acuerdo con las habitaciones que se desea que contenga.
- Inicie el laberinto extremadamente conectado (laberinto sin paredes, excepto el exterior del laberinto).
- Elija en forma aleatoria cualquier esquina de una celda a la que ninguna pared sea adjunto. Si no hay esquinas, pare, el laberinto está terminado.
- Si es posible, levantar una pared de la esquina a una esquina cercana, al azar, siempre que la esquina cercana sea parte de una pared –conecta una pared a una ya existente.
- Indique la entrada y salida del laberinto.
Desarrollo
Introducción a laberintos ampliados
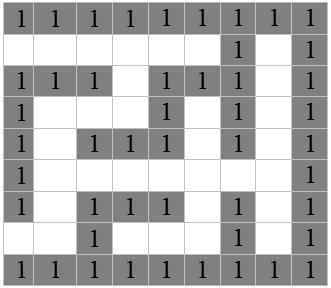
La representación matricial en “0” y “1”, del laberinto final de cada algoritmo de construcción; permite representar a las celdas libres en blanco, celdas ocupadas de color, para indicar la posición (i, j) dentro del laberinto se utiliza en su totalidad le celda respectiva de la matriz, en la fig. 3 se indica con un color distinto la entrada E y salida S del laberinto [1].
Se puede mantener la misma estructura del laberinto con más celdas libres internas (ver fig. 4).
Como se observa, el tamaño de la matriz sufre cambios con respecto al número de filas y columnas, en este tipo de laberinto se tienen más opciones de movimiento una vez abandonado la celda inicial, como se indica en la fig. 5.
Fig. 3. Representación matricial del laberinto
Fig. 4. Laberinto con ampliación 2
Fig. 5. Laberinto con ampliación 3
Se puede aumentar la ampliación, para obtener nuevos laberintos ampliados, de tal manera que se conserva la estructura del laberinto independientemente del algoritmo de construcción aplicado, lo que es una ventaja, ya que permite conocer la estructura del laberinto y por lo tanto la orientación en la ubicación de la salida, además, los laberintos ampliados tienen mayor movilidad permitiendo tener más direccionalidad respecto a los laberintos de una sola vía.
Algoritmo “LCSyM Ampliados” para la generación de laberintos
En el proceso de ampliar un laberinto, las dimensiones del arreglo cambian dependiendo de la ampliación deseada [1]. Para hacer este tipo de laberinto, se utilizan dos variables que controlan el número de filas y columnas del laberinto ampliado.
fa=(f*(ampliación+1)+1) (3)
ca=(c*(ampliación+1)+1) (4)
Las ecuaciones (3) y (4) se utilizan para calcular las filas y columnas de un laberinto ampliado, f y c son las dimensiones del arreglo inicial que se eligen en el paso 1 de los algoritmos de construcción, (ver fig. 2 paso 1). La variable “ampliación” es el número de celdas libres requeridas para los pasillos. Es necesario conocer la ampliación a priori.
Para calcular las filas y columnas de la representación matricial:
frp=f+(f+1) (5)
crp=c+(c+1) (6)
Fig. 6. Matriz para construir un laberinto con ampliación 3 de 17*17
Fig. 7. Matriz para representar un laberinto de una sola vía de 9*9
Usando (3) y (4) se obtienen los valores de las filas y columnas para el laberinto ampliado, la matriz es la que se muestra en la fig. 6. Usando (5) y (6) se calculan las filas y columnas de la matriz para realizar la representación matricial del laberinto, (ver fig. 7).
Estas matrices se modifican internamente conforme se ejecutan los pasos del algoritmo de construcción respectivo, para ejemplificar el caso se toma el algoritmo de construcción Prim´s.
El siguiente paso es “hacer” los muros del laberinto, para ello se traza la parte exterior e interior del laberinto, conforme a la ampliación deseada.
Para el ejemplo que se desarrolla, se empieza en la misma posición que se da en la Tabla 1. Los movimientos básicos en la construcción son: arriba, abajo, derecha e izquierda, las operaciones a realizar, se resumen en la Tabla 1.
Tabla 1. Movimientos realizados para construir un laberinto ampliado
En el proceso de construcción del laberinto, se van manipulando internamente las matrices (ver figs. 8 y 9), de tal manera que los movimientos realizados en el arreglo inicial de f * c, también se ven reflejados en éstas matrices.
A continuación se muestran los resultados obtenidos en las matrices en los primeros 4 movimientos realizados en el proceso de construcción del algoritmo de Prim´s, (ver fig. 2), la manipulación de la posiciones [i, j] de los arreglos se calculan al aplicar las formulas resumidas en la tabla 1.
Fig. 8. Modificaciones parciales de la representación matricial.
a) Movimiento arriba, b) Movimiento derecha, c) Movimiento abajo, d) Movimiento izquierda.
Aplicando algoritmo de Prim´s
a) Movimiento arriba
b) Movimiento derecha
c) Movimiento abajo
d) Movimiento izquierda
Fig. 9. Modificaciones parciales de la matriz del laberinto ampliado. Aplicando algoritmo de Prim´s
Fig. 10. Matriz final de la representación matricial
Fig. 11. Matriz final del laberinto con pasillos ampliados
Fig. 12. Laberinto con ampliación 3 y solución indicada
La construcción continúa hasta terminar el proceso de construcción del algoritmo Prim´s. El resultado final en la representación matricial “0” y “1” se muestra en la fig. 10, el laberinto ampliado se muestra en la fig. 11, la entrada y salida en tamaño igual al de la ampliación.
El laberinto ampliado con una posible solución indicada, la entrada y salida se reduce a una celda, este último paso se muestra en la fig. 12.
Pseudocódigo del algoritmo para ampliar un laberinto
Laberinto _ ampliado (f, c, ampliación)
{
Este algoritmo, construye un laberinto ampliado, para ello se utilizan tres arreglos bidimensionales.
M1 Matriz en donde se construye el laberinto inicial aplicando el algoritmo de construcción
M2 Matriz que contiene la representación en 0 y 1 de M1.
M3 Matriz en donde se construye laberinto ampliado.
f es el número de filas.
c es el número de columnas.
ampliación es la ampliación deseada.
i y j es la posición fila, columna de partida en la Matriz 1
}
ancho ← ampliación + 1
{Dimensiones de la Matriz 1}
M1[f][c]
{filas y columnas de la Matriz 1}
fM1 ← f + (f+1)
cM1 ← c + (c+1)
{Dimensiones de la Matriz 2}
M2[fM1] [ cM1]
{filas y columnas de la Matriz 3}
fM3 ← ( f * ( ancho + 1) ) +1
cM3 ← ( c * ( ancho + 1) ) +1
{Dimensiones de la Matriz 3}
M3[fM3] [ cM3]
{
Se hacen dos llamadas a un subprograma para trazar los muros internos de las matrices M2 y M3}
Hacer_muros(M2,2,fM1,cM1)
Hacer_muros(M3,ancho,fM3,cM3)
{
El tipo de movimiento es que se realiza en el algoritmo de construcción y básicamente son 4.
1.- Izquierda.
2.- Arriba.
3.- Derecha.
4.- Abajo.
}
Hacer tipoMovimiento←Algoritmo _Construcción
Si tipoMovimiento igual
1: Hacer
{Movimiento a la Izquierda}
im← i +(i + 1)
jm← j +( j+1)
M1[im][jm-1] ←0
ia ← ( i * ancho) + 1
jm ←( j* ancho)
limf←ia+ampliación
Mientras (ia
Hacer:
M2[ia][ja] ← 0
ia←ia +1
Fin_Mientras
2: Hacer
{Movimiento hacia Arriba}
im← i +(i + 1)
jm← j +( j+1)
M1[im]-1[jm] ←0
ia ← ( i * ancho)
limc←ja+ampliación
Mientras (ja
Hacer:
M2[ia][ja] ← 0
ja←ja +1
Fin_Mientras
3: Hacer
{Movimiento a la Derecha}
im← i +( i + 1)
jm← j +( j+1)
M1[im][jm+1] ←0
ia ← ( i * ancho) + 1
jm ←( j* ancho)
limf←ia+ampliación
Mientras (ia
Hacer:
M2[ia][ja] ← 0
ia←ia +1
Fin_Mientras
4: Hacer
{Movimiento hacia Abajo}
im← i +(i + 1)
jm← j +( j+1)
M1[im+1][jm] ←0
ia ← ( i+1) * ancho
jm ←( j* ancho) +1
limc←ja+ampliación
Mientras (ja
Hacer:
M2[ia][ja] ← 0
ja←ja +1
Fin_Mientras
Fin si tipoMovimiento igual
Mientras tipoMovimiento<>-1
Fin Laberinto_Ampliado.
Hacer _ muros (Ar, muro, nfilas, ncolumnas)
{
Este subprograma traza los muros internos en un arreglo
i, j son variables de tipo entero.
}
Hacer i←0
Repetir con i desde 0 hasta nfilas
Si (i mod muro = 0)
Hacer i←0
Repetir con j desde 0 hasta ncolumnas
Ar[i][j] ←1
Fin_Repetir
Fin_Si
Fin_Repetir
Hacer j←0
Repetir con j desde 0 hasta ncolumnas
Si ( j mod muro = 0)
Hacer i←0
Repetir con i desde 0 hasta nfilas
Ar[i][j] ←1
Fin_Repetir
Fin_Si
Fin_Repetir
Fin Hacer_Muros.
Resultados
La representación de cada celda al graficar en pantalla, varía desde el valor mínimo de 1 pixel hasta m pixeles, si el resultado final del laberinto rebasa el tamaño de la pantalla, automáticamente se ajusta este valor. Una de las características del sistema desarrollado es que permite almacenar los laberintos, dando la posibilidad de volver a “reproducir” una prueba de interés y ver el comportamiento del usuario durante el recorrido.
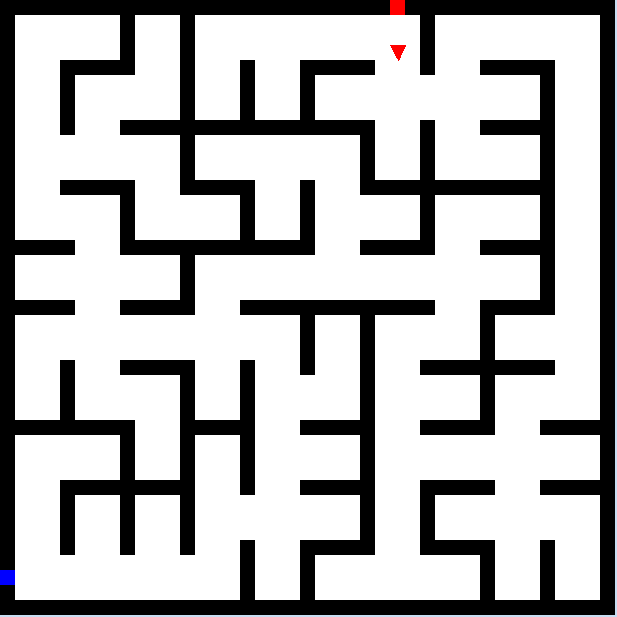
Fig. 13. Laberinto con ampliación = 5, celda=10 pixeles
Fig. 14. Laberinto con ampliación =9, celda=8 pixeles
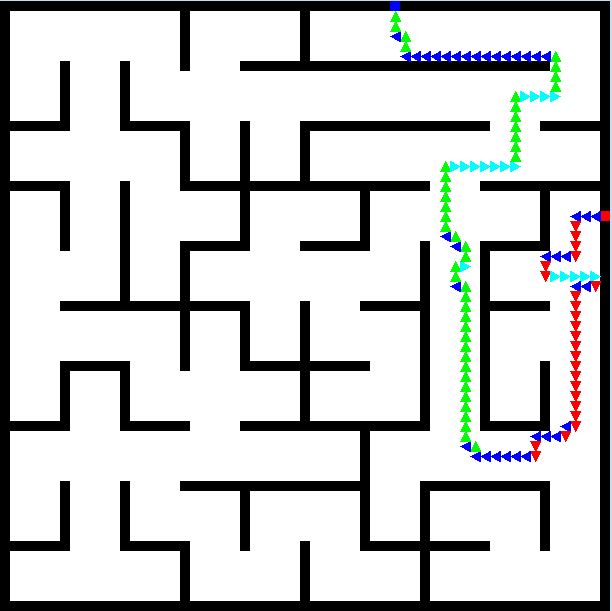
En la fig. 13 Se visualiza el recorrido realizado por el usuario desde el punto inicial con un cuadro de color rojo, y con un cuadro de color azul el punto final, los movimientos se visualizan de la siguiente manera: derecha de color azul, abajo de color rojo, a la izquierda de color cian, y arriba de color verde, esta característica permite volver a reproducir y realizar un análisis posterior a la prueba realizada por el usuario.
En la fig. 14 se muestra la posición actual del usuario, el movimiento realizado se resalta al cambiar el color del indicador, observe que se puede girar en una sección muy pequeña del laberinto ampliado, ver también la fig. 15.
Fig. 15. Laberinto con ampliación=3, celda=20 pixeles
Fig. 16. Laberinto con ampliación =21, celda=40pixeles
En la fig. 16 En este laberinto se resalta el grosor de las paredes, se observa que al dar un hurgamiento visual se identifica claramente el punto de partida y el de salida del laberinto.
En la fig. 17 se muestra un laberinto mucho más complejo, debido a que no se ubica de manera visual la entrada y salida del laberinto, haciendo más complicado el proceso de iniciar el recorrido.
Fig. 18. Laberinto con ampliación=5, celda=4 pixel
En la fig. 18 se muestra un laberinto con la entrada en un extremo y el punto final en la parte interna, por lo tanto para salir del laberinto, es necesario “regresar” al punto de partida, el objetivo es alcanzar el punto que se marca como final, en las competencias para robots móviles se utiliza este tipo de laberintos.
Posibles aplicaciones
Una de las aplicaciones de los laberintos es en la rehabilitación neuropsicológica, los laberintos son pruebas de gran utilidad para la detección de déficit de atención y síndrome frontal. Permiten evaluar diferentes niveles de integración nerviosa y trastornos específicos como secuela de una lesión cerebral [3] -[5].
La robótica es una las áreas en donde el problema de planeación de trayectorias en ambientes o espacios abiertos dinámicos tiene gran aplicación, en ocasiones se cuenta con obstáculos extras en el camino, en estos casos, el robot se auxilia de sensores para su detección y con la implementación de algoritmos que brindan información local, se puede encontrar una solución [8]-[10].
El conocimiento de la estructura del laberinto por donde se mueve el robot es de gran importancia ya que se debe tomar en cuenta la forma del propio robot para la planeación de trayectorias. En este sentido, se profundizo en los algoritmos que se aplican a laberintos de estructura conocida [8] [10] [11].
Conclusión
Los resultados arrojados por el algoritmo propuesto permiten generar laberintos ampliados de diferentes tamaños y complejidades, totalmente conectados y perfectos.
El proceso de buscar una solución en un laberinto ampliado es más complejo, se tienen diferentes rutas que conectan la entrada y salida; como complemento a este trabajo se está analizando una propuesta para encontrar la conexión de la entrada-salida; permitiendo dar una posible solución del laberinto. Garantizando que la solución dada sea segura, es decir, libre de colisiones.
Se desea medir la diferencia entre el recorrido realizado por el usuario y la solución generada por el sistema con el objetivo de medir el grado de error presentado en secciones del laberinto.
Referencias
[1] Tomás M.V.T. “Generación y Ampliación de Laberintos”, Tesis Maestría, Pachuca de Soto, CITIS, Hidalgo, México, 2007.
[2] Bernabe S. E. “Construcción y Recorrido de Laberintos”, Tesis Licenciatura, UAEH, CITIS, Hidalgo, México, Julio 2004.
[3] Domínguez R. O. A., López M. V., Samperio L. R., “Resultados Preliminares sobre Interacción Háptica en Laberintos Virtuales, con Propósitos de Diagnóstico en Pacientes con Discapacidades Neuropsicológicas”, UAEH, CITIS, Hidalgo México, 2005.
[4] Pozas C. M. J., L. H. Roberto, “Generación de Laberintos para Aplicaciones Neuropsicológicas”. CITIS, Hidalgo, México, 2006.
[5] Pozas C. M. J., L. Rojas V., Domínguez O., Tomás M. V. T., “Los Juegos Abstractos Como Instrumentos de Evaluación de Habilidades Espaciales”, CITIS, Hidalgo, México, 2006.
[6] Moore E. F., “The Shortest Path Through a Maze”, Annals of Computation Laboratory of Harvard University, Harvard University Press, vol. 30, pp. 285-292,1959.
[7] Lee C. Y., “An Algorithm for Path Connections and its Applications”, IRE Transactions on Electronic Computers, vol. EC-10, pp. 346-365, 1961.
[8] Jan G. E., Chang K-Y., Parberry I. “A New Maze Routing Approach for Path Planning of a Mobile Robot”, IEEE International Conference on Advanced Intelligent Mechatronics (AIM 2003)
[9] Dracopoulos. D. C., “Robot Path Planning for Maze Navigation”, Brunel University, Department of Computer Science, IEEE, 1998.
[10] Fraenkel A. S., “Economic Traversal of Labyrinths”, in Mathematics Magazine, vol. 43, pp. 125-130, 1970.
[11] Gordon V. S., Matley Z., “Envolving Sparse Direction Maps for Maze Pathfinding”, California State University, Sacramento and Digital Eclipse Software, Inc. Vancouver, 1992.
[12]Pullen D. W, 15/08/2011, http://www.astrolog.org/labyrinth /algorithm.htm.
[a] Profesores Investigadores de la Universidad Autónoma del Estado de Hidalgo <<